Causal Mediation Analysis#
In the era of causal revolution, identifying the causal effect of an exposure on the outcome of interest is an important problem in many areas. Under a general causal graph, the exposure may have a direct effect on the outcome and also an indirect effect regulated by a set of mediators. An analysis of causal effects that interprets the causal mechanism contributed through mediators is hence challenging but on demand.
Analysis of Causal Effects with Causal Discovery#
Identifying the causality among variables enables us to understand the key factors that influence the target variable, quantify the causal effect of an exposure on the outcome of interest, and use these effects to further guide downstream machine-learning tasks. In the following, we detail the analysis of causal effects (ANOCE) based on causal discovery proposed by Cai et al. (2020).
Analysis of Causal Effects from Treatment#
Let \(A\) be the exposure/treatment, \(\mathbf{M}=[M_1,M_2,\cdots,M_p]^\top \) be mediators with dimension \(p\), and \(R\) be the outcome of interest. Suppose there exists a weighted DAG \(\mathcal{G}=(\mathbf{Z},B)\) that characterizes the causal relationship among \(\mathbf{Z}=[A, \mathbf{M}^\top, R]^\top \), where the dimension of \(\mathbf{Z}\) is \(d=p+2\). We next give the total effect (\(TE\)), the natural direct effect that is not mediated by mediators (\(DE\)), and the natural indirect effect that is regulated by mediators (\(IE\)) defined in Pearl (2009).
where \(do(A=a)\) is a mathematical operator to simulate physical interventions that hold \(A\) constant as \(a\) while keeping the rest of the model unchanged, which corresponds to remove edges into \(A\) and replace \(A\) by the constant \(a\) in \(\mathcal{G}\). Here, \(\mathbf{m}^{(a)}\) is the value of \(\mathbf{M}\) if setting \(do(A=a)\), and \(\mathbf{m}^{(a+1)}\) is the value of \(\mathbf{M}\) if setting \(do(A=a+1)\). Refer to \citet{pearl2009causal} for more details of ‘do-operator’.
Analysis of Causal Effects from Mediators#
We first give the definition of the natural direct effect for an individual mediator (\(DM\)).
where \(m^{(a)}_i\) is the value of \( M_i\) when setting \(do(A=a)\), \(\Omega_i=\mathbf{M}\setminus M_i\) is the set of mediators except \(M_i\), and \(o^{(a)}_i\) is the value of \(\Omega_i\) when setting \(do(A=a)\). The natural indirect effect for an individual mediator (\(IM\)) can be defined similarly.
Table of Analysis of Causal Effects#
Based on the result \(TE = DE+ IE\) in Pearl (2009) and above definitions, we summarize the defined causal effects and their relationship in Table 1 for the analysis of causal effects (ANOCE). Firstly, the causal effect of \(A\) on \(Y\) has two sources, the direct effect from \(A\) and the indirect effect via \(p\) mediators \(\mathbf{M}\) (\(M_1,\cdots, M_p\)). Next, the direct source has the degree of freedom (\(d.f.\)) as 1, while the indirect source has \(d.f.\) as \(p\) from \(p\) mediators. Note the true \(d.f.\) of the indirect effect may be smaller than \(p\), since \(A\) may not be regulated by all mediators. Then, the causal effect for the direct source is the \(DE\) and for the indirect source is the \(IE\), where the \(IE\) can be further decomposed into \(p\) \(DM\)s and each component corresponds to the natural direct effect for a specific mediator. The last row in the table shows that the \(DE\) and the \(IE\) compose the total effect \(TE\) with \(d.f.\) as \(p+1\).

ANOCE-CVAE Learner (Cai et al., 2020)#
The ANOCE-CVAE learner (Cai et al., 2020) is constrained causal structure learning method by incorporating a novel identification constraint that specifies the temporal causal relationship of variables. The code is publicly available at an anonymous repository at https://github.com/anoce-cvae/ANOCE-CVAE.
The proposed algorithm is applied to investigate the causal effects of 2020 Hubei lockdowns on reducing the spread of the coronavirus in Chinese major cities out of Hubei.
import numpy as np
import pandas as pd
import os
import pickle
from utils import *
%run train.py --data_type='realdata' --real_data_file='covid19.pkl' --epochs=100 --node_number=32 --sample_size=38 --batch_size=19 --rep_number=1
usage: train.py [-h] [--data_type {realdata,simulation,create_new}] [--real_data_file REAL_DATA_FILE]
[--simu_G_file SIMU_G_FILE] [--graph_degree GRAPH_DEGREE] [--A_type A_TYPE]
[--sample_size SAMPLE_SIZE] [--node_number NODE_NUMBER] [--seed SEED] [--rep_number REP_NUMBER]
[--epochs EPOCHS] [--batch_size BATCH_SIZE] [--k_max_iter K_MAX_ITER] [--original_lr ORIGINAL_LR]
train.py: error: argument --data_type: invalid choice: "'realdata'" (choose from 'realdata', 'simulation', 'create_new')
---------------------------------------------------------------------------
ArgumentError Traceback (most recent call last)
File D:\anaconda3\lib\argparse.py:1857, in ArgumentParser.parse_known_args(self, args, namespace)
1856 try:
-> 1857 namespace, args = self._parse_known_args(args, namespace)
1858 except ArgumentError:
File D:\anaconda3\lib\argparse.py:2066, in ArgumentParser._parse_known_args(self, arg_strings, namespace)
2065 # consume the next optional and any arguments for it
-> 2066 start_index = consume_optional(start_index)
2068 # consume any positionals following the last Optional
File D:\anaconda3\lib\argparse.py:2006, in ArgumentParser._parse_known_args.<locals>.consume_optional(start_index)
2005 for action, args, option_string in action_tuples:
-> 2006 take_action(action, args, option_string)
2007 return stop
File D:\anaconda3\lib\argparse.py:1918, in ArgumentParser._parse_known_args.<locals>.take_action(action, argument_strings, option_string)
1917 seen_actions.add(action)
-> 1918 argument_values = self._get_values(action, argument_strings)
1920 # error if this argument is not allowed with other previously
1921 # seen arguments, assuming that actions that use the default
1922 # value don't really count as "present"
File D:\anaconda3\lib\argparse.py:2450, in ArgumentParser._get_values(self, action, arg_strings)
2449 value = self._get_value(action, arg_string)
-> 2450 self._check_value(action, value)
2452 # REMAINDER arguments convert all values, checking none
File D:\anaconda3\lib\argparse.py:2506, in ArgumentParser._check_value(self, action, value)
2505 msg = _('invalid choice: %(value)r (choose from %(choices)s)')
-> 2506 raise ArgumentError(action, msg % args)
ArgumentError: argument --data_type: invalid choice: "'realdata'" (choose from 'realdata', 'simulation', 'create_new')
During handling of the above exception, another exception occurred:
SystemExit Traceback (most recent call last)
File D:\anaconda3\lib\site-packages\IPython\core\interactiveshell.py:2727, in InteractiveShell.safe_execfile(self, fname, exit_ignore, raise_exceptions, shell_futures, *where)
2726 glob, loc = (where + (None, ))[:2]
-> 2727 py3compat.execfile(
2728 fname, glob, loc,
2729 self.compile if shell_futures else None)
2730 except SystemExit as status:
2731 # If the call was made with 0 or None exit status (sys.exit(0)
2732 # or sys.exit() ), don't bother showing a traceback, as both of
(...)
2738 # For other exit status, we show the exception unless
2739 # explicitly silenced, but only in short form.
File D:\anaconda3\lib\site-packages\IPython\utils\py3compat.py:55, in execfile(fname, glob, loc, compiler)
54 compiler = compiler or compile
---> 55 exec(compiler(f.read(), fname, "exec"), glob, loc)
File D:\GitHub\Causal-Decision-Making\2_Causal_Structure_Learning\train.py:62, in <module>
60 parser.add_argument('--original_lr', type = float, default = 3e-3, help = 'Initial learning rate.')
---> 62 args = parser.parse_args()
63 print(args)
File D:\anaconda3\lib\argparse.py:1824, in ArgumentParser.parse_args(self, args, namespace)
1823 def parse_args(self, args=None, namespace=None):
-> 1824 args, argv = self.parse_known_args(args, namespace)
1825 if argv:
File D:\anaconda3\lib\argparse.py:1860, in ArgumentParser.parse_known_args(self, args, namespace)
1859 err = _sys.exc_info()[1]
-> 1860 self.error(str(err))
1861 else:
File D:\anaconda3\lib\argparse.py:2581, in ArgumentParser.error(self, message)
2580 args = {'prog': self.prog, 'message': message}
-> 2581 self.exit(2, _('%(prog)s: error: %(message)s\n') % args)
File D:\anaconda3\lib\argparse.py:2568, in ArgumentParser.exit(self, status, message)
2567 self._print_message(message, _sys.stderr)
-> 2568 _sys.exit(status)
SystemExit: 2
During handling of the above exception, another exception occurred:
AssertionError Traceback (most recent call last)
Input In [2], in <cell line: 1>()
----> 1 get_ipython().run_line_magic('run', "train.py --data_type='realdata' --real_data_file='covid19.pkl' --epochs=100 --node_number=32 --sample_size=38 --batch_size=19 --rep_number=1")
File D:\anaconda3\lib\site-packages\IPython\core\interactiveshell.py:2294, in InteractiveShell.run_line_magic(self, magic_name, line, _stack_depth)
2292 kwargs['local_ns'] = self.get_local_scope(stack_depth)
2293 with self.builtin_trap:
-> 2294 result = fn(*args, **kwargs)
2295 return result
File D:\anaconda3\lib\site-packages\IPython\core\magics\execution.py:829, in ExecutionMagics.run(self, parameter_s, runner, file_finder)
826 self._run_with_timing(run, nruns)
827 else:
828 # regular execution
--> 829 run()
831 if 'i' in opts:
832 self.shell.user_ns['__name__'] = __name__save
File D:\anaconda3\lib\site-packages\IPython\core\magics\execution.py:814, in ExecutionMagics.run.<locals>.run()
813 def run():
--> 814 runner(filename, prog_ns, prog_ns,
815 exit_ignore=exit_ignore)
File D:\anaconda3\lib\site-packages\IPython\core\interactiveshell.py:2744, in InteractiveShell.safe_execfile(self, fname, exit_ignore, raise_exceptions, shell_futures, *where)
2742 raise
2743 if not exit_ignore:
-> 2744 self.showtraceback(exception_only=True)
2745 except:
2746 if raise_exceptions:
File D:\anaconda3\lib\site-packages\IPython\core\interactiveshell.py:1972, in InteractiveShell.showtraceback(self, exc_tuple, filename, tb_offset, exception_only, running_compiled_code)
1969 if exception_only:
1970 stb = ['An exception has occurred, use %tb to see '
1971 'the full traceback.\n']
-> 1972 stb.extend(self.InteractiveTB.get_exception_only(etype,
1973 value))
1974 else:
1975 try:
1976 # Exception classes can customise their traceback - we
1977 # use this in IPython.parallel for exceptions occurring
1978 # in the engines. This should return a list of strings.
File D:\anaconda3\lib\site-packages\IPython\core\ultratb.py:585, in ListTB.get_exception_only(self, etype, value)
577 def get_exception_only(self, etype, value):
578 """Only print the exception type and message, without a traceback.
579
580 Parameters
(...)
583 value : exception value
584 """
--> 585 return ListTB.structured_traceback(self, etype, value)
File D:\anaconda3\lib\site-packages\IPython\core\ultratb.py:443, in ListTB.structured_traceback(self, etype, evalue, etb, tb_offset, context)
440 chained_exc_ids.add(id(exception[1]))
441 chained_exceptions_tb_offset = 0
442 out_list = (
--> 443 self.structured_traceback(
444 etype, evalue, (etb, chained_exc_ids),
445 chained_exceptions_tb_offset, context)
446 + chained_exception_message
447 + out_list)
449 return out_list
File D:\anaconda3\lib\site-packages\IPython\core\ultratb.py:1118, in AutoFormattedTB.structured_traceback(self, etype, value, tb, tb_offset, number_of_lines_of_context)
1116 else:
1117 self.tb = tb
-> 1118 return FormattedTB.structured_traceback(
1119 self, etype, value, tb, tb_offset, number_of_lines_of_context)
File D:\anaconda3\lib\site-packages\IPython\core\ultratb.py:1012, in FormattedTB.structured_traceback(self, etype, value, tb, tb_offset, number_of_lines_of_context)
1009 mode = self.mode
1010 if mode in self.verbose_modes:
1011 # Verbose modes need a full traceback
-> 1012 return VerboseTB.structured_traceback(
1013 self, etype, value, tb, tb_offset, number_of_lines_of_context
1014 )
1015 elif mode == 'Minimal':
1016 return ListTB.get_exception_only(self, etype, value)
File D:\anaconda3\lib\site-packages\IPython\core\ultratb.py:865, in VerboseTB.structured_traceback(self, etype, evalue, etb, tb_offset, number_of_lines_of_context)
856 def structured_traceback(
857 self,
858 etype: type,
(...)
862 number_of_lines_of_context: int = 5,
863 ):
864 """Return a nice text document describing the traceback."""
--> 865 formatted_exception = self.format_exception_as_a_whole(etype, evalue, etb, number_of_lines_of_context,
866 tb_offset)
868 colors = self.Colors # just a shorthand + quicker name lookup
869 colorsnormal = colors.Normal # used a lot
File D:\anaconda3\lib\site-packages\IPython\core\ultratb.py:799, in VerboseTB.format_exception_as_a_whole(self, etype, evalue, etb, number_of_lines_of_context, tb_offset)
796 assert isinstance(tb_offset, int)
797 head = self.prepare_header(etype, self.long_header)
798 records = (
--> 799 self.get_records(etb, number_of_lines_of_context, tb_offset) if etb else []
800 )
802 frames = []
803 skipped = 0
File D:\anaconda3\lib\site-packages\IPython\core\ultratb.py:854, in VerboseTB.get_records(self, etb, number_of_lines_of_context, tb_offset)
848 formatter = None
849 options = stack_data.Options(
850 before=before,
851 after=after,
852 pygments_formatter=formatter,
853 )
--> 854 return list(stack_data.FrameInfo.stack_data(etb, options=options))[tb_offset:]
File D:\anaconda3\lib\site-packages\stack_data\core.py:546, in FrameInfo.stack_data(cls, frame_or_tb, options, collapse_repeated_frames)
530 @classmethod
531 def stack_data(
532 cls,
(...)
536 collapse_repeated_frames: bool = True
537 ) -> Iterator[Union['FrameInfo', RepeatedFrames]]:
538 """
539 An iterator of FrameInfo and RepeatedFrames objects representing
540 a full traceback or stack. Similar consecutive frames are collapsed into RepeatedFrames
(...)
544 and optionally an Options object to configure.
545 """
--> 546 stack = list(iter_stack(frame_or_tb))
548 # Reverse the stack from a frame so that it's in the same order
549 # as the order from a traceback, which is the order of a printed
550 # traceback when read top to bottom (most recent call last)
551 if is_frame(frame_or_tb):
File D:\anaconda3\lib\site-packages\stack_data\utils.py:98, in iter_stack(frame_or_tb)
96 while frame_or_tb:
97 yield frame_or_tb
---> 98 if is_frame(frame_or_tb):
99 frame_or_tb = frame_or_tb.f_back
100 else:
File D:\anaconda3\lib\site-packages\stack_data\utils.py:91, in is_frame(frame_or_tb)
90 def is_frame(frame_or_tb: Union[FrameType, TracebackType]) -> bool:
---> 91 assert_(isinstance(frame_or_tb, (types.FrameType, types.TracebackType)))
92 return isinstance(frame_or_tb, (types.FrameType,))
File D:\anaconda3\lib\site-packages\stack_data\utils.py:172, in assert_(condition, error)
170 if isinstance(error, str):
171 error = AssertionError(error)
--> 172 raise error
AssertionError:
import seaborn as sn
import matplotlib.pyplot as plt
# Load results
with open(os.path.join('', 'ANOCE_Results.data'), 'rb') as data:
data = pickle.load(data)
# Calculate the estimated causal effects
TE, DE, IE, DM, IM = calculate_effect(data[0])
# Plot the estimated weighted adjacency matrix of B for the COVID-19 data
plt.matshow(data[0].T, cmap = 'bwr', vmin = -1, vmax = 1)
fig1 = plt.gcf()
plt.colorbar()
plt.show()
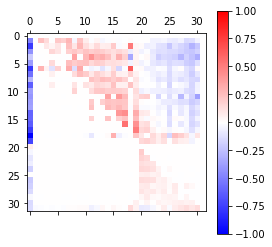
# Analysis of causal effects of 2020 Hubei lockdowns on reducing the COVID-19 spread in China regulated by Chinese major cities outside Hubei
df = pd.DataFrame()
df['cities'] = np.array(pd.read_csv("covid19.csv").columns.values[1:31])
df['DM'] = np.round(np.array(DM).reshape(-1, 1), 3)
df['IM']=np.round(np.array(IM).reshape(-1, 1), 3)
df
| cities | DM | IM | |
|---|---|---|---|
| 0 | Shenzhen | 0.212 | -0.026 |
| 1 | Guangzhou | 0.107 | 0.068 |
| 2 | Beijing | 0.039 | 0.043 |
| 3 | Chengdu | 0.084 | 0.018 |
| 4 | Shanghai | 0.018 | 0.072 |
| 5 | Dongguan | 0.072 | 0.027 |
| 6 | Suzhou | -0.072 | 0.113 |
| 7 | Xian | -0.055 | 0.045 |
| 8 | Hangzhou | -0.104 | 0.097 |
| 9 | Zhengzhou | -0.072 | 0.070 |
| 10 | Chongqing | 0.132 | 0.029 |
| 11 | Changsha | 0.079 | 0.039 |
| 12 | Nanjing | -0.101 | 0.047 |
| 13 | Kunming | -0.006 | 0.046 |
| 14 | Tianjin | -0.081 | -0.058 |
| 15 | Hefei | -0.024 | 0.076 |
| 16 | Nanning | 0.009 | 0.056 |
| 17 | Wenzhou | -0.319 | 0.033 |
| 18 | Nanchang | -0.052 | 0.001 |
| 19 | Zhoukou | 0.009 | -0.014 |
| 20 | Fuyang | 0.014 | -0.021 |
| 21 | Shangqiu | 0.008 | -0.023 |
| 22 | Yueyang | -0.002 | -0.014 |
| 23 | Zhumadian | -0.023 | -0.027 |
| 24 | Changde | 0.001 | -0.002 |
| 25 | Nanyang | -0.025 | -0.033 |
| 26 | Yichun | -0.032 | -0.025 |
| 27 | Xinyang | -0.034 | -0.018 |
| 28 | Anqing | -0.010 | -0.005 |
| 29 | Jiujiang | -0.042 | -0.020 |
# Plot the estimated (in)direct effects for selected cities.
mt_data = np.zeros((2, 30))
mt_data[0, :] = DM
mt_data[1, :] = IM
fig = plt.figure(figsize = (10, 3))
ax = fig.add_subplot()
cax = ax.matshow(mt_data, cmap = 'bwr', vmin = -1, vmax = 1)
fig.colorbar(cax,shrink = 0.4, orientation = "horizontal")
cities_name = pd.read_csv("covid19.csv").columns.values[1: 31]
ax.set_xticks(np.arange(len(cities_name)))
ax.set_yticks(np.arange(len(['DM', 'IM'])))
ax.set_xticklabels(cities_name,rotation = 90)
ax.set_yticklabels(['DM', 'IM'])
plt.show()

References#
[1] Judea Pearl et al. Causal inference in statistics: An overview. Statistics surveys, 3:96–146, 2009.
[2] Pater Spirtes, Clark Glymour, Richard Scheines, Stuart Kauffman, Valerio Aimale, and Frank Wimberly. Constructing bayesian network models of gene expression networks from microarray data. 2000.
[3] Markus Kalisch and Peter Bühlmann. Estimating high-dimensional directed acyclic graphs with the pc-algorithm. Journal of Machine Learning Research, 8(Mar):613–636, 2007.
[4] Rajen D Shah and Jonas Peters. The hardness of conditional independence testing and the generalised covariance measure. arXiv preprint arXiv:1804.07203, 2018.
[5] Shohei Shimizu, Patrik O Hoyer, Aapo Hyvärinen, and Antti Kerminen. A linear non-gaussian acyclic model for causal discovery. Journal of Machine Learning Research, 7(Oct):2003–2030, 2006.
[6] Peter Bühlmann, Jonas Peters, Jan Ernest, et al. Cam: Causal additive models, high-dimensional order search and penalized regression. The Annals of Statistics, 42(6):2526–2556, 2014.
[7] David Maxwell Chickering. Optimal structure identification with greedy search. Journal of machine learning research, 3(Nov):507–554, 2002.
[8] Joseph Ramsey, Madelyn Glymour, Ruben Sanchez-Romero, and Clark Glymour. A million variables and more: the fast greedy equivalence search algorithm for learning high-dimensional graphical causal models, with an application to functional magnetic resonance images. International journal of data science and analytics, 3(2):121–129, 2017.
[9] Xun Zheng, Bryon Aragam, Pradeep K Ravikumar, and Eric P Xing. Dags with no tears: Continuous optimization for structure learning. In Advances in Neural Information Processing Systems, pp. 9472–9483, 2018.
[10] Yue Yu, Jie Chen, Tian Gao, and Mo Yu. Dag-gnn: Dag structure learning with graph neural networks. arXiv preprint arXiv:1904.10098, 2019.
[11] Shengyu Zhu and Zhitang Chen. Causal discovery with reinforcement learning. arXiv preprint arXiv:1906.04477, 2019.
[12] Cai, Hengrui, Rui Song, and Wenbin Lu. “ANOCE: Analysis of Causal Effects with Multiple Mediators via Constrained Structural Learning.” International Conference on Learning Representations. 2020.
