Dynamic Mediation Analysis in Reinforcement Learning

Dynamic Mediation Analysis in Reinforcement Learning#

While the majority of existing works concentrate on mediation analysis with a single exposure or a limited number of treatments, there are a growing number of applications (e.g., mobile health) in which treatments are sequentially assigned over time, resulting in a large number of decision times. To learn the mediation effects in such settings with an infinite horizon, [1] proposed to construct the mediation analysis with a reinforcement learning framework. Based on a newly introduced Mediated MDP data structure as illustrated below, [1] devised a novel four-way decomposition of the average treatment effect, encompassing both long-term and short-term direct/indirect effects. A direct estimator, an IPW estimator, and a multiply-robust estimator are provided for each effect component, in accordance with the standard methodologies used in literature of off-policy evaluation (OPE).

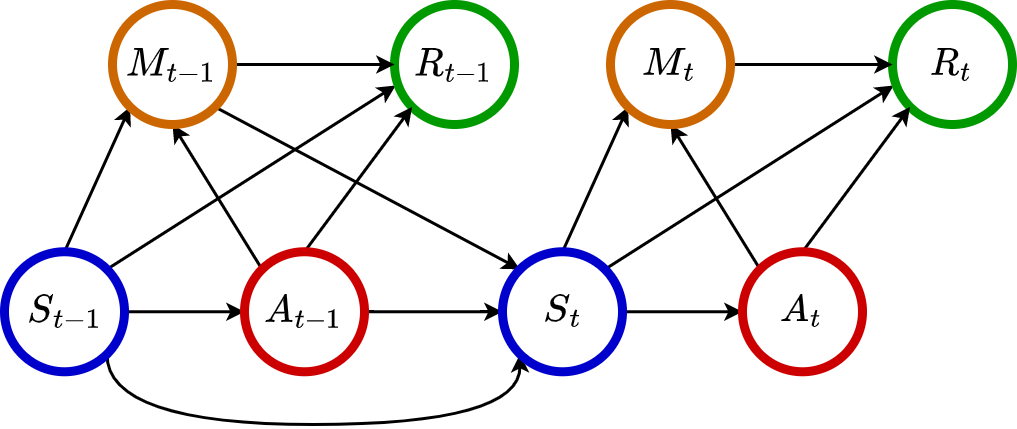
Main Idea#

The core of [1] is a four-way effect decomposition of the average treatment effect. Let $\pi_e$ denote the treatment policy of interest, where $\pi_e(a|S_t = s) = P^{\pi_e}(A_t=a|S_t=s)$, and $\pi_0$ denote the control policy. Let $E^{\pi}[\cdot]$ dentoe the expectation of a random variable under a policy $\pi$. Then the average treatment effect can be defined as

(101)#\[\begin{align} \textrm{ATE($\pi_e,\pi_0$)}=\lim_{T\to \infty} \frac{1}{T}\sum_{t=0}^{T-1} \textrm{TE$_t$($\pi_e,\pi_0$)}, \end{align}\]

where $\textrm{TE}_t(\pi_e,\pi_0) = E^{\pi_e}[R_t] - E^{\pi_0}[R_t]$. We first decompose the $\textrm{TE}_t(\pi_e,\pi_0)$ into four effect components, such that $\textrm{TE}_t(\pi_e,\pi_0) = \textrm{IDE}_t(\pi_e,\pi_0)+\textrm{IME}_t(\pi_e,\pi_0)+\textrm{DDE}_t(\pi_e,\pi_0)+\textrm{DME}_t(\pi_e,\pi_0),$ where i) the $\textrm{IDE}_t$ quantifies the direct treatment effect on the proximal outcome $R_t$; ii) the $\textrm{IME}_t$ evaluates the indirect effect mediated by $M_t$; iii) the $\textrm{DDE}_t$ quantifies how past actions directly impact the current outcome; and iv) the $\textrm{DME}_t$ measures the indirect past treatment effects mediated by past mediators.

Averaging over $t$, we obtain a four-way decomposition of ATE as $\textrm{ATE}(\pi_e,\pi_0) = \textrm{IDE}(\pi_e,\pi_0) + \textrm{IME}(\pi_e,\pi_0) + \textrm{DDE}(\pi_e,\pi_0) + \textrm{DME}(\pi_e,\pi_0).$ As an illustration, let’s consider $t=1$. The complete causal graph from actions to $R_1$ is depicted as follows.

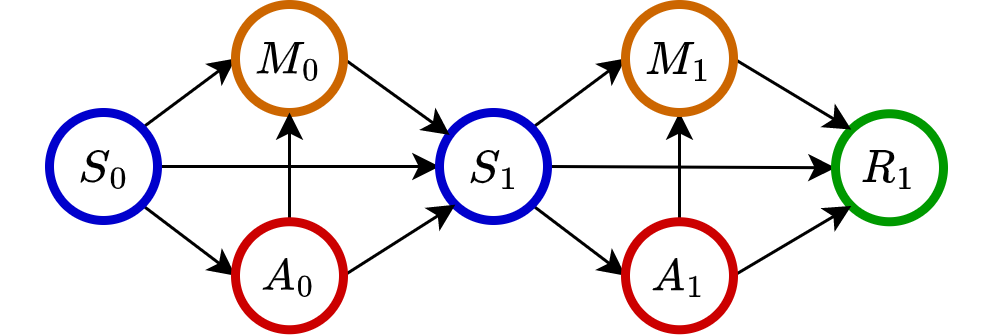
$\textrm{IDE}_1$ measures the causal effect along the path $A_1\to R_1$;
$\textrm{IME}_1$ corresponds to the effect along the path $A_1\to M_1 \to R_1$;
$\textrm{DDE}_1$ captures the causal effect along the path $A_0\to S_1\to\{A_1, M_1\}\to R_1$;
$\textrm{DME}_1$ considers the path $A_0\to M_0 \to S_1 \to \{A_1, M_1\} \to R_1$.

Each effect component is identifiable under the three standard assumptions, including consistency, sequential randomization, and positivity. Following the standard methodology used in OPE and under the assumptions, Direct estimator, IPW estimator, and multiply robust estimator for each effect component are provided in [1] and also supported by our package.

Demo Code#

Load the observational data.#

import pandas as pd
import numpy as np
import pickle
file = open('mimic3_MRL_data_dict_V2.pickle', 'rb')
mimic3_MRL = pickle.load(file)
mimic3_MRL['reward'] = [1 if r == 0 else r for r in mimic3_MRL['reward']]
mimic3_MRL['reward'] = [0 if r == -1 else r for r in mimic3_MRL['reward']]
MRL_df = pd.read_csv('mimic3_MRL_df_V2.csv')
MRL_df.iloc[np.where(MRL_df['Died_within_48H']==0)[0],-1]=1
MRL_df.iloc[np.where(MRL_df['Died_within_48H']==-1)[0],-1]=0
MRL_df[MRL_df.icustayid==1006]

	icustayid	bloc	Glucose	PaO2_FiO2	IV_Input	SOFA	next_Glucose	next_PaO2_FiO2	Died_within_48H
682	1006	1	91.0	206.000000	0	8	91.0	206.000000	1
683	1006	3	91.0	206.000000	0	8	91.0	206.000000	1
684	1006	6	175.0	100.173913	1	3	175.0	100.173913	1
685	1006	7	175.0	96.000000	1	10	175.0	96.000000	1
686	1006	8	175.0	96.000000	1	9	175.0	96.000000	1
687	1006	10	144.0	187.234036	1	12	144.0	187.234036	0

Import the learner.#

from causaldm.learners.CEL.MA import ME_MDP

Specify the control policy and the target policy#

# Control Policy
def control_policy(state = None, dim_state=None, action=None, get_a = False):
    # fixed policy with fixed action 0
    if get_a:
        action_value = np.array([0])
    else:
        state = np.copy(state).reshape(-1,dim_state)
        NT = state.shape[0]
        if action is None:
            action_value = np.array([0]*NT)
        else:
            action = np.copy(action).flatten()
            if len(action) == 1 and NT>1:
                action = action * np.ones(NT)
            action_value = 1-action
    return action_value
def target_policy(state, dim_state = 1, action=None):
    state = np.copy(state).reshape((-1, dim_state))
    NT = state.shape[0]
    pa = 1 * np.ones(NT)
    if action is None:
        if NT == 1:
            pa = pa[0]
            prob_arr = np.array([1-pa, pa])
            action_value = np.random.choice([0, 1], 1, p=prob_arr)
        else:
            raise ValueError('No random for matrix input')
    else:
        action = np.copy(action).flatten()
        action_value = pa * action + (1-pa) * (1-action)
    return action_value

Specify Hyperparameters#

dim_state=2
dim_mediator = 1
MCMC = 50
truncate = 50
problearner_parameters = {"splitter":["best","random"], "max_depth" : range(1,50)},
ratio_ndim = 10
scaler = 'Identity'
method = "Robust"
seed = 0
r_model = "OLS"
Q_settings = {'scaler': 'Identity','product_tensor': False, 'beta': 3/7, 
              'include_intercept': False, 
              'penalty': 10**(-4),'d': 2, 'min_L': 5, 't_dependent_Q': False}

Define the estimation function#

Robust_est = ME_MDP.evaluator(mimic3_MRL, r_model = r_model,
                     problearner_parameters = problearner_parameters,
                     ratio_ndim = ratio_ndim, truncate = truncate, l2penalty = 10**(-4),
                     target_policy=target_policy, control_policy = control_policy, 
                     dim_state = dim_state, dim_mediator = dim_mediator, 
                     Q_settings = Q_settings,
                     MCMC = MCMC,
                     seed = seed, nature_decomp = True, method = method)
Robust_est.estimate_DE_ME()

Building 0-th basis spline (total 3 state-mediator dimemsion) which has 3 basis, in total 3 features 
Building 1-th basis spline (total 3 state-mediator dimemsion) which has 3 basis, in total 6 features 
Building 2-th basis spline (total 3 state-mediator dimemsion) which has 3 basis, in total 9 features 

Obtain the estimation of each effect component#

Robust_est.est_IDE, Robust_est.IME, Robust_est.DDE, Robust_est.DME, Robust_est.TE

(-0.01810020554867914,
 0.006066387156687134,
 -0.004866328022066192,
 -0.00018158807389352197,
 -0.017081734487951722)

Obtain the standard error of each effect component#

Robust_est.IDE_se, Robust_est.IME_se, Robust_est.DDE_se, Robust_est.DME_se, Robust_est.TE_se

(0.0058689011135968135,
002110278954293422,
002770561709572756,
0010678186846614852,
005821662648181514)

Interpretation: We analyze the average treatment effect (ATE) of a target policy that provides IV input all of the time compared to a control policy that provides no IV input at all. Using the multiply-robust estimator proposed in [1], we decomposed the ATE into four components, including immediate nature dierct effect (INDE), Immediate nature mediator effect (INME), delayed nature direct effect (DNDE), and delayed nature mediator effect (NDDNME), and estimated each of the effect component. The estimation results are summarized in the table below.

INDE	INME	DNDE	DNME	ATE
-.0181(.0059)	.0061(.0021)	-.0049(.0028)	-.0002(.0011)	-.0171(.0058)

Specifically, the ATE of the target policy is significantly negative, with an effect size of .0171. Diving deep, we find that the DNME and DNDE are insignificant, whereas the INDE and INME are all statistically significant. Further, taking the effect size into account, we can conclude that the majority of the average treatment effect is directly due to the actions derived from the target treatment policy, while the part of the effect that can be attributed to the mediators is negligible.

References#

[1] Ge, L., Wang, J., Shi, C., Wu, Z., & Song, R. (2023). A Reinforcement Learning Framework for Dynamic Mediation Analysis. arXiv preprint arXiv:2301.13348.