Functional-based Learner#

Causal discovery attracts more and more attention recently to infer causal structure from data and disentangles the complex relationship among variables. In the following, we detail a state-of-the-art causal discovery learner, ICA-LiNGAM (Shimizu et al., 2006), as a functional-based learner.

Application situations:

  1. The noises are non-Gaussian.

  2. The functional form among nodes is pre-specified.

Advantage of the learner:

  1. Handle non-linear causal graph with non-Gaussian noises;

  2. Graph can be uniquely identified in various cases;

  3. Results are invariant to data trasformation.

Disadvantage of the learner:

  1. Cannot handle data with Gaussian noises;

  2. Require prior knowledge on the functional form.

Main Idea:#

1. Causal Graph Terminology and Goal#

Consider a graph \(\mathcal{G} =(\mathbf{Z},\mathbf{E})\) with a node set \(\mathbf{Z}\) and an edge set \(\mathbf{E}\). A node \(Z_i\) is said to be a parent of \(Z_j\) if there is a directed edge from \(Z_i\) to \(Z_j\). Let the set of all parents of node \(Z_j\) in \(\mathcal{G}\) as \(PA_{Z_j} (\mathcal{G})\). A directed graph that does not contain directed cycles is called a directed acyclic graph (DAG). Suppose a DAG \(\mathcal{G}=(\mathbf{Z},\mathbf{E})\) that characterizes the causal relationship among \(|\mathbf{Z}|=d\) nodes, where \(\mathbf{Z}=[Z_1,Z_2,\cdots,Z_d]^\top \) represents a random vector and an edge \(Z_i\rightarrow Z_j\) means that \(Z_i\) is a direct cause of \(Z_j\). Given realizations of the variable set \(\mathbf{Z}\) as \(\{z_1^{(i)},z_2^{(i)},\cdots,z_d^{(i)}\}_{1\leq i \leq n}\), we aim to estimate the underlying causal graph \(\mathcal{G}\).

2. Applicable Causal Graphical Models#

Model 1: Linear-Non-Gaussian Structural Equation Model#

Let \(B=\{b_{i,j}\}_{1\leq i\leq d,1\leq j\leq d}\) be a \(d\times d\) matrix, where \(b_{i,j}\) is the weight of the edge \(Z_i\rightarrow Z_j \in \mathbf{E}\), and \(b_{i,j}=0\) otherwise. Then, we say that \(\mathcal{G} =(\mathbf{Z},B)\) is a weighted DAG with the node set \(\mathbf{Z}\) and the weighted adjacency matrix \(B\) (the edge set \(\mathbf{E}\) is nested in \(B\)). Under no unmeasured confounders, the Markov condition, the faithfulness condition, causal sufficiency assumption, and the linear structural equation model (LSEM) such that \(\mathbf{Z}\) characterized by the pair (\(\mathcal{G}\), \(\epsilon\)) is generated by

(8)#\[\begin{equation}\label{lsem_x} \mathbf{Z}=B^\top \mathbf{Z} +\epsilon, \end{equation}\]

where \(\epsilon \) is a random vector of jointly independent error variables. In addition, under the linear model with non-Gaussian noise, the model is also identifiable (Shimizu et al., 2006).

Model 2: Non-Gaussain Additive Noise Model#

Suppose there exists a weighted DAG \(\mathcal{G}=(\mathbf{Z},\mathbf{E})\) that characterizes the causal relationship among \(|\mathbf{Z}|=d\) nodes. Each variable \(Z_i\) is associated with a node \(i\) in the DAG \(\mathcal{G}\), and the observed value of \(Z_i\) is obtained as a function of its parents in the graph plus an independent additive noise \(n_i\), i.e.,

(9)#\[\begin{equation}\label{anm} Z_i := f_i\{PA_{Z_i} (\mathcal{G})\} + n_i,i = 1,2,...,d, \end{equation}\]

where \(PA_{Z_i} (\mathcal{G})\) denotes the set of parent variables of \(Z_i\) so that there is an edge from \(Z_j\in PA_{Z_i} (\mathcal{G})\) to \(Z_i\) in the graph, and the noises \(n_i\) are assumed to be jointly independent and non-Gaussain. Assuming the \(g_j\) are three times differentiable and not linear in any of its arguments, this model is identifiable (Peters et al., 2014, Corollary 31). Here, Model 1 is a special case of Model 2 as well.

3. Algorithm Details#

The ICA-LiNGAM (Shimizu et al., 2006) algorithm assumes linear non-Gaussian additive model (Model 1 above) for data generating procedure and applies Independent Component Analysis (ICA) to recover the weighted adjacency matrix, followed by thresholding on the weights before outputting the inferred graph. The ICA-LiNGAM is implemented with default hyper-parameters through the lingam package for all settings. See their repository at https://github.com/cdt15/lingam.

Demo Code#

Generate Synthetic Datasets#

import os
import numpy as np
from utils import *
from synthetic_datasets import *
seed = 1234
np.random.seed(seed)
d = 8
n = 300
ground_truth_G = simulate_random_dag(d=d, degree=2, graph_type='erdos-renyi', w_range = (1.0, 1.0))
c = np.zeros(d)
s = np.ones([d])
df = simulate_lsem(G = ground_truth_G, A_type ='Gaussian', n = n, baseline=0).reshape((n,d))

#plot true causal graph:
plot_net(nx.to_numpy_array(ground_truth_G), labels_name=list(range(d))) 

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Input In [1], in <cell line: 4>()
      2 import numpy as np
      3 from utils import *
----> 4 from synthetic_datasets import *
      5 seed = 1234
      6 np.random.seed(seed)

ModuleNotFoundError: No module named 'synthetic_datasets'

Causal Discovery by ICA-LiNGAM Algorithm#

# ! pip install igraph
# ! pip install lingam
# ! pip install factor_analyzer
import lingam
from utils import *
model = lingam.DirectLiNGAM()
model.fit(df.reshape(len(df),d)) 
graph = model.adjacency_matrix_
ica_res = np.matrix(graph).T
ica_res[np.abs(ica_res) < 0.3] = 0 
#plot the estimated causal graph:
plot_net(ica_res, labels_name=list(range(d))) 

FDR, TPR, SHD = count_accuracy(nx.DiGraph(ground_truth_G), nx.DiGraph(ica_res))
print('FDR:', np.round(FDR, 2)) 
print('TPR:', np.round(TPR, 2)) 
print('SHD:', np.round(SHD, 2)) 

/opt/anaconda3/lib/python3.8/site-packages/statsmodels/tsa/base/tsa_model.py:7: FutureWarning: pandas.Int64Index is deprecated and will be removed from pandas in a future version. Use pandas.Index with the appropriate dtype instead.
  from pandas import (to_datetime, Int64Index, DatetimeIndex, Period,
/opt/anaconda3/lib/python3.8/site-packages/statsmodels/tsa/base/tsa_model.py:7: FutureWarning: pandas.Float64Index is deprecated and will be removed from pandas in a future version. Use pandas.Index with the appropriate dtype instead.
  from pandas import (to_datetime, Int64Index, DatetimeIndex, Period,
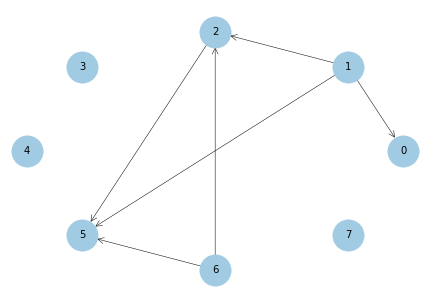
../_images/c5052d439aeb5f87fe72d685d2b22a3688acac1354906f08f94d90c4c401e7a9.png 
FDR: 0.67
TPR: 0.25
SHD: 7

Summary of Results under Different Causal Graph Learners.#

Note: The estimated graphs (after pruning) are evaluated by three metrics: the false discovery rate (FDR), the true positive rate (TPR), and the structural Hamming distance (SHD, the smallest number of edge additions, deletions, and reversals to convert the estimated graph into the true DAG). Here, the SHD takes into account both false positives and negatives and a lower SHD indicates a better estimate of the causal graph.

Learners

FDR

TPR

SHD

PC

0.00

0.50

4

ICA-LiNGAM

0.67

0.25

7

NOTEARS

0.00

0.62

3

DAGGNN

0.00

0.62

3

References#

[1] Judea Pearl et al. Causal inference in statistics: An overview. Statistics surveys, 3:96–146, 2009.

[2] Pater Spirtes, Clark Glymour, Richard Scheines, Stuart Kauffman, Valerio Aimale, and Frank Wimberly. Constructing bayesian network models of gene expression networks from microarray data. 2000.

[3] Markus Kalisch and Peter Bühlmann. Estimating high-dimensional directed acyclic graphs with the pc-algorithm. Journal of Machine Learning Research, 8(Mar):613–636, 2007.

[4] Rajen D Shah and Jonas Peters. The hardness of conditional independence testing and the generalised covariance measure. arXiv preprint arXiv:1804.07203, 2018.

[5] Shohei Shimizu, Patrik O Hoyer, Aapo Hyvärinen, and Antti Kerminen. A linear non-gaussian acyclic model for causal discovery. Journal of Machine Learning Research, 7(Oct):2003–2030, 2006.

[6] Peter Bühlmann, Jonas Peters, Jan Ernest, et al. Cam: Causal additive models, high-dimensional order search and penalized regression. The Annals of Statistics, 42(6):2526–2556, 2014.

[7] David Maxwell Chickering. Optimal structure identification with greedy search. Journal of machine learning research, 3(Nov):507–554, 2002.

[8] Joseph Ramsey, Madelyn Glymour, Ruben Sanchez-Romero, and Clark Glymour. A million variables and more: the fast greedy equivalence search algorithm for learning high-dimensional graphical causal models, with an application to functional magnetic resonance images. International journal of data science and analytics, 3(2):121–129, 2017.

[9] Xun Zheng, Bryon Aragam, Pradeep K Ravikumar, and Eric P Xing. Dags with no tears: Continuous optimization for structure learning. In Advances in Neural Information Processing Systems, pp. 9472–9483, 2018.

[10] Yue Yu, Jie Chen, Tian Gao, and Mo Yu. Dag-gnn: Dag structure learning with graph neural networks. arXiv preprint arXiv:1904.10098, 2019.

[11] Shengyu Zhu and Zhitang Chen. Causal discovery with reinforcement learning. arXiv preprint arXiv:1906.04477, 2019.

[12] Cai, Hengrui, Rui Song, and Wenbin Lu. “ANOCE: Analysis of Causal Effects with Multiple Mediators via Constrained Structural Learning.” International Conference on Learning Representations. 2020.

[13] J. Peters and P. Bühlmann. Identifiability of Gaussian structural equation models with equal error variances. Biometrika, 101(1):219–228, 2013.

[14] J. Peters, J. Mooij, D. Janzing, and B. Schölkopf. Causal Discovery with Continuous Additive Noise Models. Journal of Machine Learning Research, 2014.